Maxwell's equations

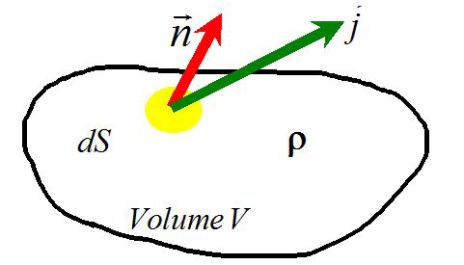
Let us consider a volume \((V)\) delimited by a closed surface \((S)\) (set in the referential of the study).

Let \(\rho\) be the charge density in the setting.

The total charge \(Q(t)\) included in the volume at the moment \(t\) is equal to :

\(Q(t) = \iiint_{(V)}\rho \;d\tau\)

The electric charge conservation law allows us to write :

\(\frac{{dQ}}{{dt}} = - i(t)\)

Consequently :

\(\frac{d}{dt}(\iiint_{(V)}\rho\; d\tau)\ = - \oint_{(S)}\vec {j}.\vec{n} \ dS\)

Because the volume \((V)\) is steady :

\(\frac{d}{dt}(\iiint_{(V)}\rho d\tau)\ =\iiint_{(V)}\frac{\partial \rho}{\partial t} d\tau\)

Finally, the principle of charge conservation leads to :

\(\iiint_{(V)}\frac{\partial \rho}{\partial t} d\tau=- \oint_{(S)}\vec {j}.\vec{n} \ dS\)

By using Green - Ostrogradsky's law :

\(\iiint_{(V)}\frac{\partial \rho}{\partial t} d\tau=- \oint_{(S)}\vec {j}.\vec{n} \ dS=-\iiint_{(V)} div\vec{j} \ d\tau\)

So :

\(\iiint_{(V)}(\frac{\partial \rho}{\partial t} +div\vec{j})\ d\tau=0\)

This result is true for any volume \((V)\), so:

\(div\vec{j}+\frac{\partial \rho}{\partial t} =0\)

It is the local charge conservation law.