Charge of a capacitor and energy review
Take 15 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel free to ask them on the forum.
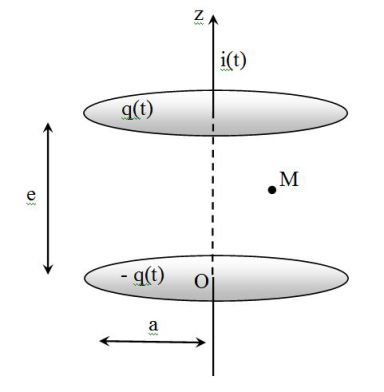
Let us model a plane capacitor by two metal discs of radius \(a\).
They are parallel and separated by a distance \(e\).
The upper disc has a charge \(q(t)\) and the other has a charge \(-q(t)\).
We suppose \(e<<a\) (border effects are neglected).
The capacitor is charged by a time-dependent exterior current \(i(t)\).
The capacitance is :
\(C=\frac {\varepsilon_0 \pi a^2}{ e}\)
Question
Show that the electric field inside the capacitor is :
\(\vec E(t)=-\frac{q(t)}{\varepsilon_0 \pi a^2}\vec u_z\)
Indice
Think about symmetry and invariances.
Solution
The electric field outside a capacitor is equal to zero.
Let M be a point located between the two frames.
If the two frames are considered infinite, the electric potential only depends on variable \(z\), being \(V(z)\). The electric field is oriented by (Oz) axis.
\(\vec E = - \overrightarrow {grad} V(z) = - \frac{{dV(z)}}{{dz}}{{\vec u}_z}\)
Poisson's equation :
\(\Delta V(z) = - \frac{\rho }{{{\varepsilon _0}}}\;\;\;\;\;\;\;gives\;\;\;\;\;\;\;\frac{{{d^2}V(z)}}{{d{z^2}}} = 0\)
The density of charge is equal to zero between the two frames.
Hence the potential \(V(z)\) is a linear function of \(z\), and the electric field is constant between the two frames.
In order to use Gauss' law, let's choose a cylinder of vertical axis (Oz).
Its upper base, of same surface as the two frames, crosses point M. Its lower base is located under the inferior frame, where the electric field is equal to zero.
Gauss' law :
\( \oint_{(S)}\vec {E}.\vec{n} \ dS=\frac{Q_{int}}{\varepsilon_0}\)
Thus :
\(SE = \pi {a^2}E = \frac{{ - q(t)}}{{{\varepsilon _0}}}\)
The field is thus equal to :
\(\vec E(t)=-\frac{q(t)}{\varepsilon_0 \pi a^2}\vec u_z\)
Question
Show that a magnetic field appears. We will suppose that it can be expressed by :
\(\vec B(r,t)=B(r,t)\; \vec u_{\theta}\)
Determine it as a function of \(dq(t)/dt\), and using one of Maxwell's equations.
Solution
Local equation of Maxwell-Ampere :
\(\overrightarrow {rot} (\vec B) = {\mu _0}(\vec j + {\varepsilon _0}\partial \vec E/\partial t)\)
In the absence of volume currents inside the capacitor, this equation becomes :
\(\overrightarrow {rot} (\vec B) = {\mu _0}{\varepsilon _0}\; \partial \vec E/\partial t\)
Hence, the existence of an electric field which depends on time explains the presence of a magnetic field inside the capacitor.
The source of the magnetic field is the displacement currents which correspond to the variation of the electric field over time.
The magnetic field belongs to the anti-symmetry planes of the distribution which hold point M.
It is also perpendicular to the other symmetry planes which hold point M, as for instance the plane \((M,\vec u_r,\vec u_{z})\): hence it is carried by \(\vec u_{\theta}\).
Because of the cylindrical symmetry, the problem is invariant by rotation around \((Oz)\) axis : the field is thus independent of \(\theta\) :
\(\vec B(M,t) = B(r,z){\vec u_\theta }\)
\(\oint_{(C)} {\vec B.} d\vec \ell =\epsilon_0 \mu_0 \iint_{(S)}\frac{{\partial \vec E}}{{\partial t}}.\vec n\; dS\)
Let's compute the magnetic field in a point inside the capacitor.
By applying Stokes theorem to a circle of radius \(r<a\) and oriented like \(\vec u_{\theta}\) :
\(\oint_{(C)} {\vec B.} d\vec \ell = 2\pi rB(r,z) = \iint_{(S)}\frac{{\partial \vec E}}{{\partial t}}.\vec n\; dS = - \frac{{{\varepsilon _0}{\mu _0}}}{{\epsilon_0\pi {a^2}}}\frac{{dq(t)}}{{dt}}\pi {r^2}\)
Thus, inside the capacitor :
\({\vec B_{{\mathop{\rm int}} }}(M,t) = -\frac{{{\mu _0}}}{{\pi {a^2}}}\frac{{dq(t)}}{{dt}}\frac{r}{2}{\; \vec u_\theta }\)
Question
Compute Poynting's vector. Evaluate its flux entering the capacitor.
Interpret the results.
Solution
Poynting's vector is :
\(\vec \Pi = \frac{{\vec E \wedge \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftarrow$}}\over B} }}{{{\mu _0}}} = - \frac{{q(t)}}{{{{(\pi {a^2})}^2}}}\frac{{dq(t)}}{{dt}}\frac{r}{{2{\varepsilon _0}}}\; {\vec u_r}\)
Poynting's vector is oriented towards the inside of the capacitor.
Indeed, the energy goes inside the capacitor which is charging.
The flux of Poynting's vector through the lateral surface of the capacitor is :
\(\Phi=\oint \vec {\Pi}.\vec n\; dS=2\pi ae\Pi (r=a)\)
Hence :
\(\Phi=- e\frac{{q(t)}}{{\pi {a^2}}}\frac{{dq(t)}}{{dt}}\frac{1}{{{\varepsilon _0}}}\)
The capacity of the plane capacitor is :
\(C=\frac {\varepsilon_0 \pi a^2}{e}\)
By noticing that :
\(q(t)\frac{{dq(t)}}{{dt}} = \frac{d}{{dt}}\left( {\frac{1}{2}q{{(t)}^2}} \right)\)
Finally :
\(\Phi=- \frac{d}{{dt}}\left( {\frac{1}{{2C}}q{{(t)}^2}} \right)\)
Is similar in this expression :
\({E_{em}} = \frac{1}{2}\frac{{q(t)_{}^2}}{C}\)
Is the energy stored by a capacitor during its charge.
The previous equation can be written as :
\(\Phi = -\frac {dE_{em}}{dt}\)
The power that enters the capacitor is given by Poynting's vector.
It corresponds indeed to the electric power received by the capacitor during its charge.
It could also have been evaluated in a classical manner with electro-kinetic laws.