Group velocity of a wave packet
Exemple : Propagation of two harmonic progressive plane waves of close frequencies
It is assumed that the wave vector is real (it does not take into account the absorption).
\(k_1=k(\omega_1)\) and \(k_2=k(\omega_2)\) are the real wave vectors of the two waves.
It is assumed that the frequencies \(\omega_1\) and \(\omega_2\) are close and let :
\({\omega _0} = \frac{{{\omega _1} + {\omega _2}}}{2}\;\;\;\;\;\;\;;\;\;\;\;\;\;\;{k_0} = \frac{{{k_1} + {k_2}}}{2}\;\;\;\;\;\;\;;\;\;\;\;\;\;\;\delta \omega = {\omega _1} - {\omega _2}\;\;\;\;\;\;\;;\;\;\;\;\;\;\;\delta k = {k_1} - {k_2}\)
With \(\left| {\delta \omega } \right| < < {\omega _0}\) and \(\left| {\delta k} \right| < < {k_0}\).
It further assumes that the two waves have the same amplitude.
The resulting wave, superposition of two waves, has for amplitude :
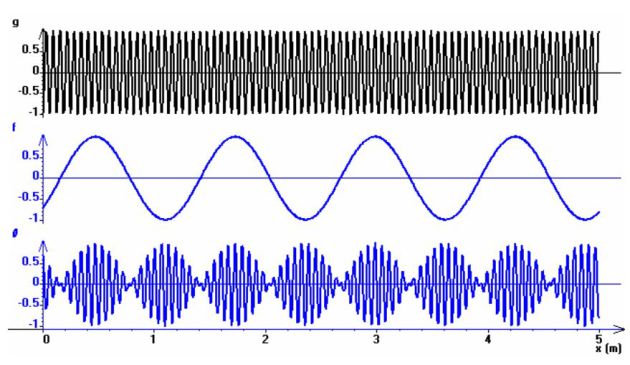
\(\theta (x,t) = A\cos ({\omega _1}t - {k_1}x) + A\cos ({\omega _2}t - {k_2}x) = 2A\cos \left( {\frac{{\delta \omega }}{2}t - \frac{{\delta k}}{2}x} \right)\;\cos ({\omega _0}t - {k_0}x)\)
Beats are observed (Figure below) : an average wave vector \(k_0\) is enveloped by an envelope wave of wave vector \(\delta k\).
Over time, the average waveform (upper in the figure) is a progressive plane wave of speed \(\omega_0 /k_0\) whereas the envelope wave (the middle one) is a plane wave of velocity \(\delta \omega /\delta k\).
These speeds are not identical in general, the average wave crests advance at a speed different from that of the crests of the envelope wave.
Fondamental : Extension to the case of a wave packet
Wave packet is called a set of harmonic progressive plane waves of close frequencies.
More precisely, their frequencies are in the range \(\left[ {{\omega _0} - \frac{{\Delta \omega }}{2},{\omega _0} + \frac{{\Delta \omega }}{2}} \right]\), with \(\Delta \omega <<\omega_0\).

The resulting wave can be written as a Fourier integral :
\(\underline \theta (x,t) = \int_{\; - \infty }^{\; + \infty } {} \underline A (\omega )\;\exp \left[ {j(\omega t - k(\omega)x)} \right]\;d\omega\)
Where the amplitude \(A(\omega)\) takes only notable values over the interval \(\left[ {{\omega _0} - \frac{{\Delta \omega }}{2},{\omega _0} + \frac{{\Delta \omega }}{2}} \right]\).
By making a \(1st\) order expansion :
\(k(\omega ) = {k_0} + {\left( {\frac{{dk}}{{d\omega }}} \right)_{{\omega _0}}}(\omega - {\omega _0})\)
It comes, replacing \(\omega = {\omega _0} + (\omega - {\omega _0})\) :
\(\underline \theta (x,t) = \int_{\; - \infty }^{\; + \infty } {} \underline A (\omega )\;\exp \left[ {j({\omega _0}t - {k_0}x)} \right]\exp \left[ {j(\omega - {\omega _0})(t - x{{\left( {\frac{{dk}}{{d\omega }}} \right)}_{{\omega _0}}})} \right]\;d\omega\)
Hence :
\(\underline \theta (x,t) = \exp \left[ {j({\omega _0}t - {k_0}x)} \right]\;\left\{ {\int_{\; - \infty }^{\; + \infty } {} \underline A (\omega )\;\exp \left[ {j(\omega - {\omega _0})(t - x{{\left( {\frac{{dk}}{{d\omega }}} \right)}_{{\omega _0}}})} \right]\;d\omega } \right\}\)
Let :
\(\underline E (t - x{\left( {\frac{{dk}}{{d\omega }}} \right)_{{\omega _0}}}) = \;\int_{\; - \infty }^{\; + \infty } {} \underline A (\omega )\;\exp \left[ {j(\omega - {\omega _0})(t - x{{\left( {\frac{{dk}}{{d\omega }}} \right)}_{{\omega _0}}})} \right]\;d\omega\)
Finally :
\(\underline \theta (x,t) = \underline E (t - x{\left( {\frac{{dk}}{{d\omega }}} \right)_{{\omega _0}}})\;\exp \left[ {j({\omega _0}t - {k_0}x)} \right]\;\)
Here we see an average wave \(\exp \left[ {j({\omega _0}t - {k_0}x)} \right]\) of frequency \(\omega_0\) propagating phase velocity :
\({v_\varphi } = \frac{{{\omega _0}}}{{{k_0}}}\)
and an envelope wave \(\underline E (t - x{\left( {\frac{{dk}}{{d\omega }}} \right)_{{\omega _0}}})\) depends only on the variable :
\(t - x{\left( {\frac{{dk}}{{d\omega }}} \right)_{{\omega _0}}} = t - x/{\left( {\frac{{d\omega }}{{dk}}} \right)_{{\omega _0}}}\)
and which propagates at the velocity called group velocity :
\({v_g} = {\left( {\frac{{d\omega }}{{dk}}} \right)_{{\omega _0}}}\)
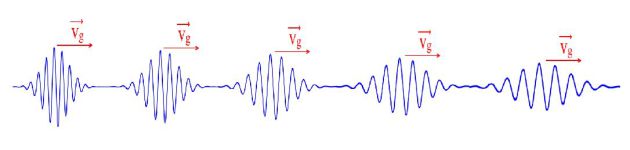
The phase and group velocities are a priori different and the wave packet spreads by deforming.
Indeed, each of the monochromatic components of the group "walks" with its own speed, so we observe a deformation of the whole wave packet along its spread.
We also appreciated that this deformation is accompanied by a spreading of the wave packet due to increasing taken by the components of high speed.
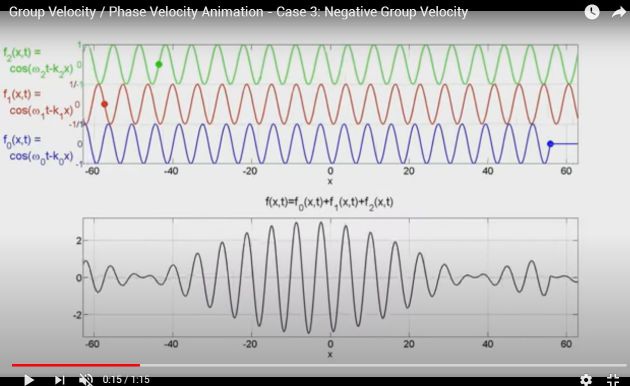
Complément : A video about the significance of the group velocity
Attention : Phase velocity and group velocity
For a real wave, which is the superposition of monochromatic progressive plane waves propagating in any medium, it is possible to define two speeds :
The phase velocity :
\({v_\varphi } = \frac{\omega }{k}\)
It corresponds to the phase propagation velocity of a monochromatic component.
It has no physical reality, that is to say does not correspond to a power transmission.
Group velocity :
\({v_g} = \frac{{d\omega }}{{dk}}\)
It is the speed of the propagation of the envelope of the wave.
It shows that it is usually identified with the speed of propagation of energy (or information).
The principle of relativity requires that the group velocity is less than the speed of light in vacuum.
If \(v_{\varphi}\) effectively dependent of \(\omega\), then the phase of each sinusoidal progressive plane wave propagates at its own speed.
A real physical wave, consisting of sinusoidal progressive plane waves, will deform during its propagation : this is called dispersion.