Reflection of a wave on a "perfect" metal, radiation pressure (wave calculation)
Spend 20 minutes to prepare for this exercise.
Then, if you run out of ideas for starting, see the supplied index and start searching.
A detailed solution is then proposed.
If you have further questions, feel free to ask them on the forum.
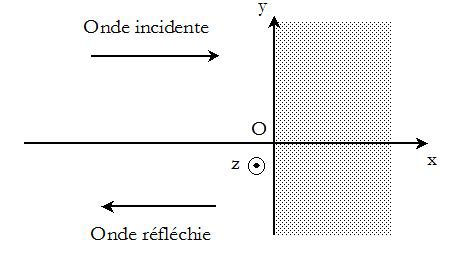
A MPPW, linearly polarized, propagates in the vacuum in the (Ox) axis, in the direction of increasing \(x\) (assuming \(E_0>0\)) :
\(\underline {\vec E} _i = E_0 e^{j(\omega t - kx)} \vec e_y\)
At \(x=0\), it arrives on the plane surface of a metal mirror perfectly conducting, in which the fields \(\vec E\) and \(\vec B\) are zero, and gives birth to a reflected wave propagating in the direction of decreasing \(x\) :
\(\underline {\vec E} _r = E_{0r} e^{j(\omega t + kx)} \vec e_y\)
Question
By writing the boundary conditions that must check the fields \(\vec E\) and \(\vec B\) in \(x=0\), determine :
The amplitude \(E_{0,r}\) of the field reflected according to \(E_0\).
The surface charge \(\sigma\) and the surface current \(\vec j_s\) that can be found on the metal surface at \(x=0\).
Indice
What are the boundary conditions of an electromagnetic wave passing through a perfect metal ?
Solution
The tangential component of the electric field should be continuous, therefore :
\({E_{0r}} = - {E_0}\)
The boundary condition for the electric field :
\({\vec E_{metal}(0^+,t)} - {\vec E_{vide}(0^-,t)} = - {\vec E_{vide}(0^-,t)} = \frac{\sigma }{{{\varepsilon _0}}}{\vec u_x}\)
Show that \(\sigma =0\).
The boundary condition for the magnetic field gives :
\({\vec B_{metal}(0^+,t)} - {B_{vide}(0^-,t)} = - {\vec B_{vide}(0^-,t)} = {\mu _0}{\vec j_s} \wedge {\vec u_x}\)
The incident magnetic field is :
\({\underline {\vec B} _i} = \frac{{{{\vec e}_x}}}{c} \wedge {\underline {\vec E} _i} = \frac{{{{\vec e}_x}}}{c} \wedge {E_0}{e^{j(\omega t - kx)}}{\vec e_y} = \frac{{{E_0}}}{c}{e^{j(\omega t - kx)}}{\vec e_z}\)
The reflected magnetic field is :
\({\underline {\vec B} _r} = - \frac{{{{\vec e}_x}}}{c} \wedge {\underline {\vec E} _r} = \frac{{{{\vec e}_x}}}{c} \wedge {E_0}{e^{j(\omega t + kx)}}{\vec e_y} = \frac{{{E_0}}}{c}{e^{j(\omega t + kx)}}{\vec e_z}\)
The resulting field in the vacuum for \(x=0^-\) is :
\({\vec B_{vide}}(0^-,t) = {({\underline {\vec B} _i} + {\underline {\vec B} _r})_{x=0^-}} = 2\frac{{{E_0}}}{c}{e^{j\omega t}}{\vec e_z}\)
We can deduce :
\({\vec B_{vide}(0^-,t)} = 2\frac{{{E_0}}}{c}{e^{j\omega t}}{\vec e_z} = - {\mu _0}{\vec j_s} \wedge {\vec u_x}\;\;\;\;\;\;\;\;\;\;so\;\;\;\;\;\;\;\;\;\;{\vec j_s} = 2\frac{{{E_0}}}{{{\mu _0}c}}{e^{j\omega t}}{\vec e_y} = 2{\varepsilon _0}c{E_0}{e^{j\omega t}}{\vec e_y}\)
Real notation :
\({\vec j_s} = 2{\varepsilon _0}c{E_0}\cos (t){\;\vec e_y}\)
Question
Determine the resulting electromagnetic field of the incident wave and the reflected wave in the half-space \(x<0\).
Briefly characterize the resulting wave.
Calculate the average value of the Poynting vector.
Indice
The total field is the sum of the initial field and reflected.
What is a standing wave ?
Solution
The resultant electric field is :
\(\vec E = {E_0}{e^{j(\omega t - kx)}}{\vec e_y} - {E_0}{e^{j(\omega t + kx)}}{\vec e_y} = - 2j{E_0}\sin (kx){e^{j\omega t}}{\vec e_y}\)
Either in real notation :
\(\vec E = 2{E_0}\sin (kx)\sin (\omega t){\;\vec e_y}\)
Similarly, for the magnetic field :
\(\vec B = {\underline {\vec B} _i} + {\underline {\vec B} _r} = \frac{{{E_0}}}{c}{e^{j(\omega t - kx)}}{\vec e_z} + \frac{{{E_0}}}{c}{e^{j(\omega t + kx)}}{\vec e_z} = 2\frac{{{E_0}}}{c}\cos (kx){e^{j\omega t}}{\vec e_z}\)
Either in real notation :
\(\vec B = 2\frac{{{E_0}}}{c}\cos (kx)\cos (\omega t){\;\vec e_z}\)
This type of solutions, called standing plane wave is very different from a progressive plane wave. Spatial and temporal dependencies occur separately : spatial dependence occurs in the amplitude of the time oscillation and no longer in phase, so that all points vibrate in phase or in opposition of phase.
At certain points (called nodes of vibrations), the field is always zero.
In other points (called vibration antinodes), the amplitude of vibration is maximum.
We can calculate Poynting vector and verify that its average value is zero : a standing wave does not transport energy.
Question
The electromagnetic field exerted on a mirror surface \(dS\) a force \(\vec {dF}\) whose expression is, in real notation :
\(d\vec F = \frac{1}{2}\left( {\sigma \vec E + \vec j_s \wedge \vec B} \right)dS\)
Offer an explanation for the presence of the factor \(1/2\).
Derive that the wave exerts a pressure \(p\) on the mirror whose average value \(<p>\) will be calculated as the function of the average energy density \(e_i\) of the incident wave (\(p\) is called radiation pressure).
Solution
The electromagnetic field exerted on a mirror surface \( dS\) a force \(d\vec F\) whose expression is, in a real notation : (note that \(\sigma =0\))
\(d\vec F = \frac{1}{2}{\vec j_s} \wedge \vec B\;dS\)
Indeed, the surface \(dS\) is subjected to the action of the magnetic field external to it ; so do not take into account the magnetic field created by the charged surface \(dS\) and traveled by volume current.
The factor \(1/2\) takes into account the remarks.
The average value of the force becomes :
\(\left\langle {d\vec F} \right\rangle = \frac{1}{2}{\mathop{\rm Re}\nolimits} \left( {\frac{1}{2}{{\vec j}_s} \wedge {{\vec B}^*}dS} \right) = \frac{1}{4}(2{\varepsilon _0}c{E_0}{e^{j\omega t}}{\vec e_y}) \wedge (2\frac{{{E_0}}}{c}{e^{ - j\omega t}}{\vec e_z})dS = {\varepsilon _0}E_0^2{\;\vec e_x}\;dS\)
The average radiation pressure is then :
\(\left\langle p \right\rangle = {\varepsilon _0}E_0^2\)
The volumetric energy density of the incident wave is :
\({e_i} = \frac{1}{2}{\varepsilon _0}{E_i^2} + \frac{1}{2}\frac{{{B_i^2}}}{{{\mu _0}}}\)
Whose average value is :
\(\left\langle {{e_i}} \right\rangle =\frac{1}{2} {\varepsilon _0}E_0^2\)
We can deduce the radiation pressure :
\(\left\langle p \right\rangle = {\varepsilon _0}E_0^2 = 2 \left\langle {{e_i}} \right\rangle\)
We can notice that :
\(\left\langle p \right\rangle = {\varepsilon _0}E_0^2 = 2 \left\langle {{e_i}} \right\rangle = 2n^*h\nu\)
Where \(n^*\) is the density of photons of the incident wave and \(h\nu\) the energy of one photon.