Current density vector and intensity
Fondamental :
The system considered is a set of particles of charge \(q\).
Its particular density is \(n^*\) and the average drift velocity is \(\vec v\).
Let :
\(\rho_m=n^*q\)
be the density of mobile charges.
How can the intensity going through a given surface \(dS\) be defined ?
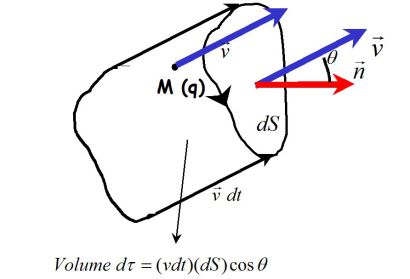
The amount of electric charges \(dq\) going through the elementary surface \(dS\) during the time \(dt\) is :
\(dq = n^* d\tau \;q = n^* (dS\cos \theta \;vdt)\;q\)
Yet :
\(vdScos\theta=\vec v.\vec ndS\)
Thus :
\(dq = n^* (\vec v.\vec n\;dS)\;qdt = \vec j.\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}}\over n} \;dS\;dt\)
We have defined the current density vector :
\(\vec j = n^* q\;\vec v = \rho _m \vec v\)
The intensity \(di\) :
\(di = \frac{{dq}}{{dt}} = \vec j.\vec n\;dS\)
can be interpreted as the flux of the current density vector through the oriented surface \(dS\).
The intensity passing through the finite surface \((S)\) becomes :
\(i = \iint_S\vec j.\vec n\;dS\)
Attention : Definition of intensity
The current intensity is interpreted as the surface integral of current density vector through the oriented surface \(S\) :
\(i = \iint_S\vec j.\vec n\;dS\)
Complément : Differences between volume and surface models
For a current density :
\(\vec j = \rho \vec v\;\;\;\;\;;\;\;\;\;\;di = \vec j.\vec ndS\)
For a surface current repartition :
\(\vec j = \sigma \vec v\;\;\;\;\;;\;\;\;\;\;di = \vec j.\vec nd\ell\)
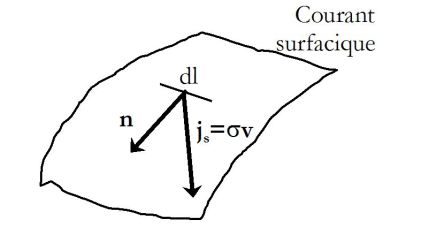
Instead of counting the charges passing through a given surface, we count the charges that cross a segment of length \(d\ell\) of normal vector \(\vec n\).