Hall Effect
Fondamental : Action of a magnetic field on the movement of charge carriers
An electrical conductor under a voltage difference sees its carrier electrons set in motion.
The lesson about Ohm's local law specified the notations.
The electrical conductor is additionally placed in a magnetic field \(\vec B\).
Newton's second law applied to a charge carrier is expressed by :
\(m\frac{{d\vec v}}{{dt}} = q(\vec E + \vec v \wedge \vec B) - k\vec v\;\;\;\;\;so\;\;\;\;\;\frac{{d\vec v}}{{dt}} + \frac{1}{\tau }\vec v = \frac{q}{m}(\vec E + \vec v \wedge \vec B)\)
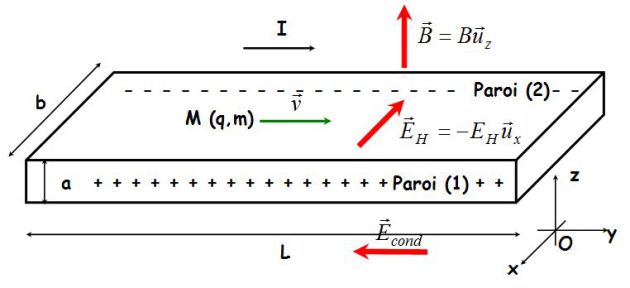
The following picture outlines the geometry of the conductor used : it is a parallelepiped rectangle of length \(L\).
The exterior magnetic field is \(\vec B = B \vec u_z\).
The electric field created by the generator which sets charge carriers in motion is called \(\vec E_e\).
In steady-state, electrons move with the velocity \(\vec v = v \vec u_y\).
In steady-state (\(t>>\tau\)) :
\(\vec v = \frac{{\tau q}}{m}(\vec E + \vec v \wedge \vec B)\)
The magnetic term \(q \vec v \wedge \vec B\) is oriented as Ox axis. Thus an electric field appears, called the Hall field \(\vec E_H\) such as :
\(\vec E=\vec E_e+\vec E_H\)
With :
\(\vec E_H+\vec v \wedge \vec B = \vec 0\)
Thus, the speed of the carriers becomes :
\(\vec v = \frac{{\tau q}}{m}\vec E_e\)
This Hall field is induced by the motion of electrons during a brief moment (length of transitory regime) towards side (2).
This creates a dissymmetry of charges, thus an electric field oriented from side (1) to side (2).
Fondamental : Calculation of the Hall Voltage
The Hall electric field is :
\({\vec E_H} = - \vec v \wedge \vec B = - v\;{\vec u_y} \wedge B\;{\vec u_z} = - vB\;{\vec u_x}\)
The Hall voltage \(\Delta V_H\) is obtained by calculating the line integral around a loop of the field :
\(\int_0^{ - b} {{{\vec E}_H}.dx\;{{\vec u}_x}} = \int_0^{ - b} {( - vB\;{{\vec u}_x}).dx\;{{\vec u}_x}} = vbB = - ({V_2} - {V_1}) = {V_1} - {V_2} = \Delta {V_H}\)
Thus :
\(\Delta {V_H} = vbB\)
The intensity of the current is :
\(I = jab = nqvab\)
Consequently :
\(\Delta {V_H} = \frac{I}{{nqab}}bB = \frac{1}{{nq}}\frac{{IB}}{a}\)
If \(q=-e\) (carrier electrons case, with \(I<0\) on the picture) :
\(\Delta {V_H} = - \frac{1}{{ne}}\frac{{IB}}{a} = - {R_H}\frac{{IB}}{a}\;\;\;\;\;\;(with\;{R_H} = \frac{1}{{ne}},\;Hall's\;constante)\)
Hence we can see the Hall voltage is proportional to the magnetic field that is applied.
Hall probes can measure this voltage and deduce the value of the magnetic field.
Complément : Laplace force
See the lesson about Laplace force.