Bohr's model
Fondamental : Bohr's assumptions
The hydrogen atom is composed of a proton O (of mass \(M\) and electric charge \(+e\)) and of an electron P (of mass \(m<<M\) and charge \(–e\)).
The electron travels around the proton in a circular orbit of radius \(r\).
The proton is supposed stationary and at the origin of a Galilean referential (that of the laboratory).
The only force considered here is the Coulomb interactive force between the two charges.
Bohr's assumptions are :
Steady orbits exist (also called stationary orbits) for which the electron does not radiate any energy.
The electron absorbs or radiates energy only when travelling from one stationary orbit to another.
How can these stationary orbits be characterized ?
Bohr proved that, through conditions imposed by his assumptions, stationary orbits were those for which the kinetic moment of the electron was an integer multiple of a constant \(\hbar\), equal to \(h/2\pi\), where \(h\) is planck's constant.
Hence, if \(L_O\) is the kinetic moment of the electron (or angular momentum) on a stationary orbit, in relation to the proton then :
\(L_O=n\hbar\)
Where \(n\) is a positive integer.
Fondamental : Mechanical study
Let's determine a relation between the radius \(r\) of the trajectory and the speed \(v\) of the electron.
Newton's second law applied to the electron in the Galilean referential of the nucleus of the atom gives, when projected on radius \(OP\) :
\(m\frac{{{v^2}}}{r} = \frac{{{e^2}}}{{4\pi {\varepsilon _0}}}\frac{1}{{{r^2}}}\)
Hence :
\(v = \sqrt {\frac{{{e^2}}}{{4\pi {\varepsilon _0}}}\frac{1}{{mr}}}\)
The kinetic energy \(E_c\), the potential energy \(E_p\) and the mechanical energy \(E_m\) of the electron can be expressed as functions of \(r\) and constants \(e\) and \(\varepsilon_0\) :
\({E_c} = \frac{1}{2}m{v^2} = \frac{1}{2}\frac{{{e^2}}}{{4\pi {\varepsilon _0}}}\frac{1}{r}\;\;\;;\;\;\;{E_p} = - \frac{{{e^2}}}{{4\pi {\varepsilon _0}}}\frac{1}{r}\;\;\;;\;\;\;{E_p} =E_c+E_p= -\frac{1}{2} \frac{{{e^2}}}{{4\pi {\varepsilon _0}}}\frac{1}{r}\)
Fondamental : Quantification of angular momentum, radii and atom energies
To interpret the spectral rays of the hydrogen atom, Bohr's model constrains the electron to have a quantified kinetic moment (angular momentum) :
\({L _O} = n\hbar = n\frac{h}{{2\pi }}\)
Where \(n\) is a natural integer different from zero, and \(h\) is planck's constant.
Let us determine the radii, written \(r_n\), of the orbits allowed.
The kinetic moment of the electron in relation to the nucleus placed in O is :
\({\vec L _O} = \mathop {OP}\limits^ \to \wedge m\vec v = r{\vec u_r} \wedge mv{\vec u_\theta } = mrv{\;\vec u_z} = \sqrt {\frac{{{e^2}}}{{4\pi {\varepsilon _0}}}mr} {\;\vec u_z}\)
The condition of quantification of the kinetic moment constrained by N. Bohr leads to a quantification of radii (now written \(r_n\)) of the allowed orbits.
Indeed, the expression :
\(L _O^2 = {\hbar ^2}{n^2} = \frac{{{e^2}}}{{4\pi {\varepsilon _0}}}m{r_n}\)
gives :
\({r_n} = \left( {\frac{{4\pi {\varepsilon _0}}}{{{e^2}}}\frac{{{\hbar ^2}}}{m}} \right){n^2} = {r_0}{n^2}\;\;\;\;with\;\;\;\;{r_0} = \frac{{4\pi {\varepsilon _0}}}{{{e^2}}}\frac{{{\hbar ^2}}}{m}\)
\(r_0\) represents the radius of the orbit of the electron for \(n=1\).
The state of the electron associated to \(n=1\) is called fundamental state, and \(r_0\) is called Bohr's radius.
It can be proven that the energy of the electron is quantified and can be written as :
\({E_n} = - \frac{{{E_0}}}{{{n^2}}}\)
Actually :
\({E_n} = - \frac{1}{2}\frac{{{e^2}}}{{4\pi {\varepsilon _0}}}\frac{1}{{{r_n}}} = - \frac{1}{2}{\left( {\frac{{{e^2}}}{{4\pi {\varepsilon _0}}}} \right)^2}\frac{m}{{{\hbar ^2}}}\frac{1}{{{n^2}}} = - \frac{{{E_0}}}{{{n^2}}}\)
With :
\({E_0} = \frac{1}{2}{\left( {\frac{{{e^2}}}{{4\pi {\varepsilon _0}}}} \right)^2}\frac{m}{{{\hbar ^2}}}\)
\(E_0\) represents the mechanical energy of the electron in its fundamental state.
Numerically :
\({a_0} = {5,33.10^{ - 11}}m\;\;;\;\;{E_0} = {2,18.10^{ - 18}}J = 13,6\) \(eV\)
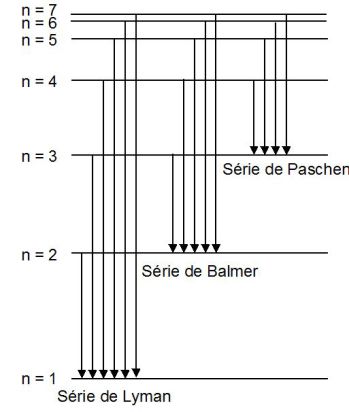
Exemple : Example of Balmer's sequence
By creating an electric discharge in a light bulb full of hydrogen gas (or dihydrogen), these molecules dissociate themselves and the excited atoms emit electromagnetic radiation of different wavelengths.
Physicist J. Balmer determined experimentally that the wavelengths \(\lambda\) of these radiations which are located in the domain of visible light, verified this phenomenological relation : (\(n\) is a positive integer)
\(\frac{1}{\lambda } = {R_H}\left[ {\left( {\frac{1}{4}} \right) - \left( {\frac{1}{{{n^2}}}} \right)} \right]\)
Where \(R_H\) is Rydberg's constant.
It is equal to \(R_H=109\;677\;cm^{-1}\).
Bohr's model can help determine the theoretical value of this constant \(R_H\) :
When the hydrogen atom goes from a level defined by the quantum number \(n\) to the state that corresponds to the quantum number \(2\), it emits a photon whose energy is given by :
\(h\nu = \frac{{hc}}{\lambda } = {E_n} - {E_2}\)
Consequently, the wavenumber (defined as the inverse of the wavelength of the emited radiation) is :
\(\frac{1}{\lambda } = \frac{1}{{hc}}\left( {{E_n} - {E_2}} \right) = \frac{{{E_0}}}{{hc}}\left( {\frac{1}{4} - \frac{1}{{{n^2}}}} \right)\)
Rydberg's constant can be interpreted as the quantity :
\({R_H} = \frac{{{E_0}}}{{hc}} = {1,09.10^7}{m^{ - 1}} = {1,09.10^5}c{m^{ - 1}}\)
Its theoretical value corresponds very well to the experimental value determined by J. Balmer.
In conclusion, Bohr's model gives the right levels of energy for the hydrogen atom.
However, the classical representation of an electron moving on a circular orbit revolving around the proton has been proved wrong by quantum mechanics.
The latter gives the image of an electron that is not located and of which can only be known the probability of presence, “materialized” by a cloud of probability (atomic orbitals) surrounding the nucleus.
Complément : Wave interpretation of Bohr's atom model
The wave of the electron can be represented as a wave running around the orbit as it would run on a rope.
After a large number of periods, the wave will, in most cases selfdestruct by interference with itself.
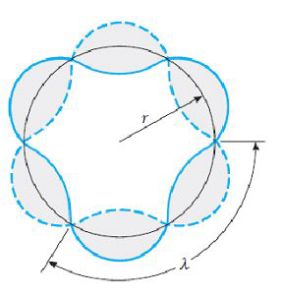
In order for the interferences not to be destructive the length of the orbit must be a multiple integer of the wavelength of the electron.
\(r_n\) is the radius of the orbit :
\(2\pi {r_n} = n\lambda \;\;\;\;\;so\;\;\;\;\;{r_n} = \frac{{n\lambda }}{{2\pi }}\)
Considering that :
\(\lambda = \frac{h}{p} = \frac{h}{{mv}}\)
We find that the angular momentum is quantified :
\(m{v_n}{r_n} = n\frac{h}{{2\pi }} = n\hbar\)
The electronic wave can help interpret the quantification of the angular momentum.