Réaliser des mesures d'optique avec un Goniomètre
Méthode : Vidéo sur le Goniomètre
Réglages du Goniomètre (lunette et collimateur) par A Le Rille
Méthode : Vidéos sur le spectrogoniomètre (Référence : lycée Louis Le Grand, Paris)
Fondamental : Étude théorique d'un réseau de diffraction
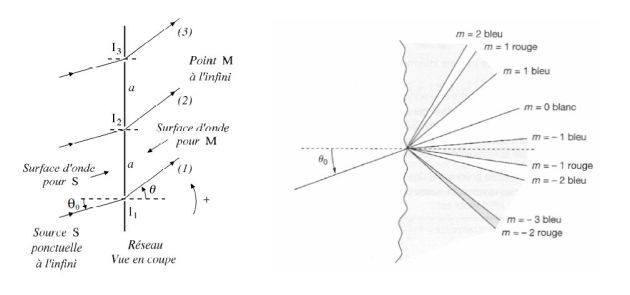
Un réseau de diffraction est un composant optique possédant une structure périodique (par exemple, un ensemble de fentes très proches les unes des autres et parallèles).
Un réseau diffracte la lumière en différents ordres que l'on retrouve dans des directions bien déterminées.

On considère un réseau de fentes, de largeur \(b\) et distantes de \(a\) (c'est le pas du réseau).
On note \(n=1/a\) le nombre de "traits" (de fentes) du réseau.
Soit \(\theta_0\) l'angle d'incidence de la lumière.
La lumière est diffractée dans certaines directions repérées par l'angle \(\theta\) donné par :
\(sin\theta - sin\theta_0=p\frac{\lambda_0}{a}\)
\(p\) est l'ordre du spectre (nombre entier relatif).
C'est la formule fondamentale des réseaux de diffraction.
Cette relation est difficilement exploitable car la normale au réseau n'est pas toujours repérable de façon précise.
La déviation des rayons, plus facilement mesurable avec un goniomètre, est alors donnée par :
\(D=\theta-\theta_0\)
Minimum de déviation :
Pour une longueur d'onde \(\lambda_0\) donnée et pour un spectre d'ordre p donné, la déviation D ne dépend que de l'angle d'incidence \(\theta_0\).
Cette déviation passe par un minimum quand \(\theta_0\) varie.
On montre qu'au minimum de déviation : (voir fiche de cours sur les réseaux de diffraction)
\(\theta \;\, = \;\, - \;\,{\theta _i}\;\, = \;\,\frac{{{D_{min}}}}{2}\;\;\;\;soit\;\;\;\;\;2\;\sin \,\,\frac{{{D_{min}}}}{2}\;\;\, = \;\,p\;\frac{\lambda }{a}\)
Cette relation est facilement exploitable car la détermination de \(D_{min}\) est aisée.
Remarque :
si l'ordre p du spectre est égal à zéro, les rayons ne sont pas déviés (la déviation est nulle quelle que soit la longueur d'onde k\lambda_0 ).
Dans ce cas, l'axe de la lunette est dans le prolongement de l'axe du collimateur.
La mesure de l'ordre p du spectre est facile : il suffit de compter combien de fois on observe une raie d'une couleur donnée en partant du spectre d'ordre zéro ( rayons non déviés).
La mesure du pas du réseau peut se faire en observant le réseau à travers un microscope.
La mesure de l'angle de déviation minimal permet :
Soit de mesurer le pas a du réseau si l'on connaît la longueur d'onde d'une raie donnée ; on peut choisir l'une des raies du doublet jaune d'une lampe spectrale au sodium.
Soit de mesurer une longueur d'onde inconnue connaissant le pas a du réseau : c'est le but de la spectroscopie.
Si l'on ne connaît pas le pas du réseau, on peut néanmoins comparer entre elles deux longueurs d'onde.
Soit une raie de longueur d'onde \(\lambda_1\) observée au minimum de déviation dans son spectre d'ordre \(p_1\) :
\(2\;\sin \,\,\frac{{{D_{mi{n_1}}}}}{2}\;\;\, = \;\,{p_1}\;\frac{{{\lambda _1}}}{a}\)
Soit une raie de longueur d'onde \(\lambda_2\) observée au minimum de déviation dans son spectre d'ordre \(p_2\) :
\(2\;\sin \,\,\frac{{{D_{mi{n_2}}}}}{2}\;\;\, = \;\,{p_2}\;\frac{{{\lambda _2}}}{a}\)
En faisant le rapport :
\(\frac{{{\lambda _2}}}{{{\lambda _1}}}\;\;\, = \;\,\frac{{{p_1}}}{{{p_2}}}\;\,\frac{{\sin \,\,\frac{{{D_{mi{n_2}}}}}{2}}}{{\sin \,\,\frac{{{D_{mi{n_1}}}}}{2}}}\)
Ainsi, si l'on connaît la première longueur d'onde, on pourra connaître la seconde.
Méthode : Principe de la mesure du minimum de déviation et mesure du pas a du réseau
Éclairer la fente du collimateur avec la lampe spectrale au sodium.
Observer une raie dans le spectre d'ordre p désiré (cela dépend du pas du réseau choisi).
Tourner la plate-forme tout en observant la raie choisie pour rendre l'angle de déviation minimal : la raie doit se rapprocher le plus possible de l'axe du collimateur.
Faire coïncider la raie choisie avec le trait vertical du réticule.
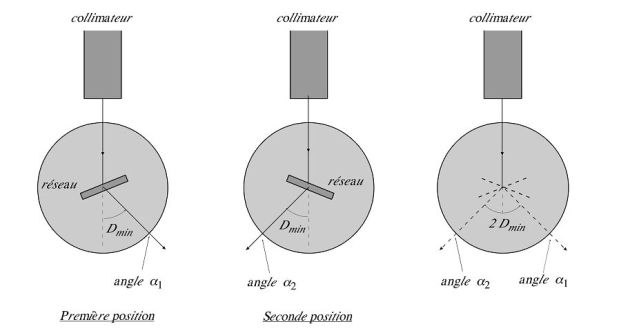
Mesurer alors la position de la lunette par rapport au support (angle \(\alpha_1\)) ; vérifier à l'œil nu que le plan du réseau est approximativement bissecteur des rayons incident et diffracté.
Tourner la plate-forme et se placer dans la position de déviation minimale symétrique (cela revient à changer \(p\) en \(-p\)).
Mesurer alors la position de la lunette par rapport au support (angle \(\alpha_2\)) ; vérifier à l'œil nu que le plan du réseau est approximativement bissecteur des rayons incident et diffracté.
En déduire l'angle de déviation minimal par :
\({D_m} = \frac{1}{2}\left| {{\alpha _2} - {\alpha _1}} \right|\)
On donne \(\lambda_1=589,0\;nm\) pour la longueur d'onde la plus petite du doublet jaune.
En déduire la valeur du pas a avec la relation :
\(2\;\sin \,\,\frac{{{D_{min}}}}{2}\;\;\, = \;\,p\;\frac{\lambda }{a}\)
Quel est le nombre de traits par mm ?
Méthode : Mesures de longueurs d'ondes inconnues en traçant la courbe d'étalonnage du spectroscope
On choisit une lampe spectrale donnant un grand nombre de raies réparties dans tout le spectre visible et de longueurs d'ondes connues.
On choisit la lampe à mercure (ne pas la regarder directement à cause des rayons ultraviolets émis).
Placer le réseau en position de déviation minimale pour une raie située environ au milieu du spectre (on choisit la raie verte du mercure dans le spectre d'ordre 1 ).
Faire coïncider chaque raie de la lampe à mercure avec le trait vertical du réticule et repérer l'angle \(\alpha\) correspondant à la position de la lunette.
Tracer la courbe d'étalonnage : angle \(\alpha\) en abscisse et longueur d'onde \(\lambda_0\) en ordonnée.
On utilisera le tableau donné à la fin de cette fiche de TP.
On va déterminer les longueurs d'onde du doublet jaune du sodium.
Mettre la lampe au sodium devant la fente du collimateur.
Mesurer les angles \(\alpha\) correspondant à chacune des raies du doublet.
En déduire leurs longueurs d'onde.
Complément : Observation des spectres de la lumière blanche
Éclairer la fente du collimateur en lumière blanche.
Observer les spectres d'ordre 0 , 1 , 2 ... en prenant des réseaux de pas différents.
Observer les éventuels chevauchements des spectres.
Attention : Longueurs d'onde des raies les plus intenses du mercure
Couleur | Longueur d'onde (en nm) |
violet | 404,7 |
indigo | 435,8 |
bleu-vert | 491,6 |
vert | 546,1 |
jaune | 576,1 et 579,0 |
orange | 623,4 |
rouge | 690,7 |