Observation of double stars
Take 10 minutes to prepare this exercise.
Then, if you lack ideas to begin, look at the given clue and start searching for the solution.
A detailed solution is then proposed to you.
If you have more questions, feel free to ask them on the forum.
Consider a source consisting of two points \(P_1\) and \(P_2\), separated by a distance \(h\).
This source illuminates two Young's holes. We note \(\lambda_0\) the common wavelength issued by the two sources and it is assumed that the waves from the two sources have the same amplitude.
This case may be, for example, the two components of a double star as seen from Earth.
This exercise highlights the concept of spatial coherence : the spatial coherence of a light source is better as long as the source is limited in space.
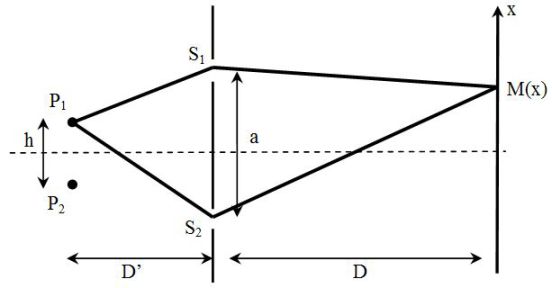
The observation is done on a remote screen shot of the two slits in the distance \(D\).
We note \(D'\) the distance from the plane of the two slits with two point sources.
Question
Determine the intensities \(I_1\) and \(I_2\) on the screen, an abscissa point \(x\), due to each of the stars.
Indice
The stars are incoherent : the total intensity on the screen will be the sum of the intensities created by each star individually.
Solution
The stars are incoherent : the total intensity on the screen will be the sum of the intensities created by each star individually.
We are interested in the illumination due to the source \(P_1\). The total path difference is :
\(\delta = ({P_1}{S_2}M) - ({P_1}{S_1}M) = \frac{{ah}}{{2D'}} + \frac{{ax}}{D}\)
The intensity is then :
\({I_1}(M) = 2{I_{0}}\left( {1 + \cos \frac{{2\pi }}{{{\lambda _0}}}\left( {\frac{{ah}}{{2D'}} + \frac{{ax}}{D}} \right)} \right)\)
In the same way, the intensity due to the second source is :
\({I_2}(M) = 2{I_{0}}\left( {1 + \cos \frac{{2\pi }}{{{\lambda _0}}}\left( { - \frac{{ah}}{{2D'}} + \frac{{ax}}{D}} \right)} \right)\)
Question
Deduce the total intensity on the screen and put in the form :
\(I_{tot} = 4I_0 \left[ {1 + V\cos \left( {\frac{{2\pi ax}}{{\lambda_0 D}}} \right)} \right]\)
What is the meaning of the term \(V\) ?
Indice
Using the trigonometric relationship :
\(\cos p + \cos q = 2cos\frac{{p + q}}{2}\cos \frac{{p - q}}{2}\)
Solution
We obtain :
\(I(M) = {I_1}(M) + {I_2}(M) = 4{I_0}\left( {1 + \cos \left( {\frac{{2\pi }}{{{\lambda _0}}}\frac{{ah}}{{2D'}}} \right)\;\cos \left( {\frac{{2\pi }}{{{\lambda _0}}}\frac{{ax}}{D}} \right)} \right)\)
It is recognized in the second cosine term interference of Young's holes for a single point source. The fringes are rectilinear and the interfringe is equal to :
\(i = \frac{{{\lambda _0}D}}{a}\)
The first cosine is independent of the observation point. It is called visibility and noted \(V\) :
\(V = \cos \left( {\frac{{2\pi }}{{{\lambda _0}}}\frac{{ah}}{{2D'}}} \right)\)
Fringes contrast is defined by :
\(\Gamma = \frac{{{I_{\max }} - {I_{\min }}}}{{{I_{\max }} - {I_{\min }}}} = \left| V \right|\)
Contrast and visibility are therefore equal to the sign.

The previous figure shows the shape of the fringes on the screen, in terms of the value of contrast \(\Gamma\).
Zero contrast is obtained for a distance \(h\) between sources such as :
\(V = \cos \left( {\frac{{2\pi }}{{{\lambda _0}}}\frac{{ah}}{{2D'}}} \right)=0\)
Take, for example :
\(\frac{{2\pi }}{{{\lambda _0}}}\frac{{ah}}{{2D'}} = \frac{\pi }{2}\;\;\;\;\;so\;\;\;\;\;h = \frac{{{\lambda _0}}}{{2a}}D'\)
One can find this particular value of \(h\) using a qualitative reasoning.
Indeed, when there is interference fringes, the light fringes due to the first star superimposed on the dark fringes due to the second star.
Therefore, unlike the orders of interference at a point \(M\) of the screen should be half-integer.
In the case where this difference is equal to \(1/2\) :
\(\frac{{{\delta _1}(M)}}{{{\lambda _0}}} - \frac{{{\delta _2}(M)}}{{{\lambda _0}}} = \frac{1}{{{\lambda _0}}}\left( {\frac{{ah}}{{2D'}} + \frac{{ax}}{D}} \right) - \frac{1}{{{\lambda _0}}}\left( { - \frac{{ah}}{{2D'}} + \frac{{ax}}{D}} \right) = \frac{1}{{{\lambda _0}}}\frac{{ah}}{{D'}} = \frac{1}{2}\)
We thus find :
\(h = \frac{{{\lambda _0}}}{{2a}}D'\)